The Independence Axiom and Expected Utility
Introduction1
The future can never be fully known.
Tomorrow could be rainy or sunny, peace or war. A new deposit of oil could be found, a new technology created.
The future is a realm where humans act the most irrationally. Psychologists provide many examples of such. Some people gamble at the casino believing in the gambler's bias — they are due to win because they have lost so many times. Others believe in the reverse, the hot-hand fallacy — they won once, they must win next time. Still others ignore all ideas of luck and chance and believe all is predetermined by some divine force.
Philosophy offers many ways to understand what will come, going back to Aristotle's four types of causes (material, formal, efficient, and final). What makes economics different, however, is that it provides a way for us to rationally decide what to do here and now. The theory of decision-making under uncertainty, one of the great intellectual triumphs of economics of the twentieth century, allows us to optimally play Blackjack, to make an optimal portfolio, to envision a moral human society, and to make a strategic foreign policy. It requires a set of assumptions, some the same as in consumer theory, one unique, the independence axiom. With them, we can know what to choose to do now even if we don't fully know what will happen in the future.
Yet, these ideas have also been subject to controversy. A powerful critique challenges the foundation of the independence axiom, the Allais Paradox. Yet the independence axiom and its expected utility result form the basis of almost all game theory and financial economics. To know is to know the basis of modern microeconomics. And so we begin with it.
Section 1: Gambles
Humans love gambles, whether Blackjack, a lottery ticket, or a stock.2 Even a strategic business or political decision is a gamble. By their nature, we cannot know what will happen beforehand when we decide what to do. One only knows that there's a probability of success or failure. It's a 1 in 292 million odds to win the jackpot in the Powerball. In a deck of 52 cards, there's a 4.8% chance you'll win Blackjack with your opening hand. I can calculate there is a 40% chance my financial portfolio will go up in the next five years, 40% will stay the same, and 20% will go down. So on, so forth.
Gambles can be simple, like the flip of a coin, or complicated, like poker. Yet, one can always reduce even the most complicated gamble down to the probabilities. After all, no matter the various cards one can pick in Blackjack, there are always two numbers you care about — the probability you win and the probability you lose. Not everything comes down to money — a gamble can also be the risk in a football play — but money is the easiest to understand.
The first and most basic assumption to analyzing the future is that we focus on the outcomes and their probabilities in a gamble. Of course, reality has multiple contingencies that could affect my portfolio — a pandemic, war, or a financial crisis. Each can cause further events that could affect my portfolio — lockdown, national defense, stimulus package. Yet, ultimately, we focus on the probabilities of my portfolio rising or falling, win or loss in negotiations and at the Blackjack table.
With that in mind, we can ask another question. Given that we only care about outcomes and probabilities, when can we use numbers to personally rank gambles? And does it have to have the same form as the functions from consumer theory? Or does expected utility theory have greater power?
Section 2: Axioms
Firstly, like consumer theory, our decision-making must have transitive and complete properties. For completeness, we can compare any two gambles to each other. Is getting a 20 in Blackjack better or worse than getting a 17? A 22? A 1?
Secondly, the transitive property says if I prefer a hand of 18 in a game of Blackjack over 17 and 17 over 16, I prefer 18 over 16. Having a different preference because my friend is playing the game, and I don't want him to lose all his money, doesn't apply here. We are all professional blackjack players.
Secondly, we need to have continuous preferences. The difference to consumer theory is that continuous preferences in the uncertainty case imply a small addition of a probability that won't change the fundamental preferences.
Take, for example, the following two gambles:
I assume everyone prefers Gamble 1A to Gamble 1B.
If you have continuous preferences, there will be a number between 0 and 1 where you still prefer 1B to 2B. Maybe it's 100 dollars with a 99.99 percent chance and 0 dollars with 0.01 percent chance – or 99% and 1% percent, or so on. The numbers are up to you. But $0 must have more than a 0% chance — you must add a small risk to Gamble 1B.
Already, we have the three rationality axioms. Theoretically, we can form the utility from consumer choice. But it doesn't make much sense to use the same utility functions for Blackjack as we use for going shopping at Costco. One of the great triumphs of the twentieth century in economics was the creation of a new type of utility: expected utility, similar to the expected outcome of probability times outcome that allows us to subjectively value gambles. For us to achieve that, we need one more specific axiom.
Section 2b. The Independence Axiom
What distinguishes the theory of uncertainty and consumer choice is the independence axiom. It says that adding or removing new probabilities and outcomes to any two gambles won't alter my preferences. If I like gamble 1 to gamble 2, adding new probabilities and outcomes to both — gamble 3 — means I still like gamble 1 to gamble 2. Indeed, even if I start with two gambles, it says that I prefer Gamble 1 to Gamble 2.
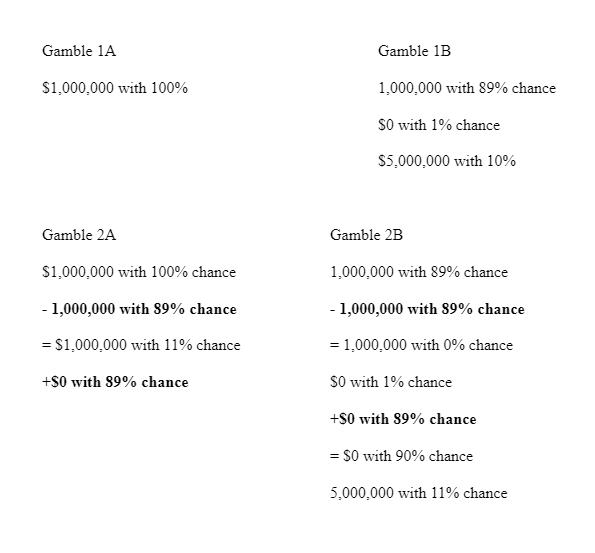
As a concrete example, imagine there are two gambles.
What would you pick? (Most, I assume, would say Gamble 1A)
Now, let's add a new lottery to both.
The independence axiom also says that we do this in reverse: if we prefer Gamble 1B to Gamble 2B, then it means we prefer Gamble 1A to Gamble 2A. We also can find them equal, of course.
The independence axiom says that adding a third, irrelevant outcome and probability cannot alter our preferences. The independence axiom is also referred to as the axiom of irrelevant alternatives.
The addition (or subtraction) of outcomes and probabilities occurs naturally in real life. My chances change in Blackjack if one of the other players gets kicked out of the game. The outbreak of a natural disaster, a pandemic, or a war alters the return of my portfolio. Yet the independence axiom requires that if everything is changed simultaneously, we should not adjust our portfolios or change our card game strategy. The world changing doesn't mean we change our decisions. If we do, we are only worsening our chances of victory.
Section 3: Expected Utility
From the independence axiom and three rationality axioms is a new utility function: expected utility.
Like the expected outcome of a dice roll, it is the expected satisfaction I get from a gamble the moment I choose it in the present. What makes it different from the expected outcome – probability times outcome – is that expected utility is probability times the personal valuation of the outcome. That personal valuation is just like the idea of a consumer's utility function. It depends on my subjective taste.
To see what that means, imagine a game called St Petersburg's Paradox in the 18th century. You flip a coin. If it comes up heads, you get $1 and flip again. If another heads, $2 and flip again—$ 4, $8, $16, and so on. If at any point you flip tails, you lose.
From the simple point of the expected outcome, without the expected utility function, one should pay anything to play this game. After all, one can obtain a million dollars. Yet it's clearly not true I would mortgage my house to play this game.
One of the great powers of expected utility is that we can gain far more information than any consumer theory utility. David Bernoulli, one of the great mathematicians of the 18th century, assumed people have log expected utility — a special type of mathematical function essentially equivalent to saying we avoid risk. With that assumption, he then showed, using the inverse of the log function, that people would bet up to $3.35 to play the gamble.
The class of expected utility I have – whether I avoid or prefer risk – affects my choice of stocks in a financial portfolio. Investors' utility affects whether the stock market is approximately normally distributed (where most returns are around the mean). Expected utility can give us the optimal strategy in a game, whether Blackjack or Poker or the Prisoner's Dilemma. It can go into the realm of philosophy and political science — the concepts of Mutually Assured Destruction (MAD), the central foreign policy of the Cold War, and John Rawl's Veil of Ignorance stem from an expected utility framework.
The four axioms lead, in other words, to the second basis of microeconomics. And much of the following articles will depend entirely on these four axioms.
Section 4: Allais Paradox
Now that we have discussed the theory of expected utility, a detour.
Say that a Frenchman comes up to you and offers you the following two gambles. He is a very rich Frenchman — a mogul of the great French grape wine — and will give you money here and now.
After making your choice, you are given a second round of gambles.
You pick your choice again. He shakes your hand, gives you your money, and leaves with an adieu.
What did you choose? For me, it would be 1A and then 2B. If you did the same (or chose 2A and then 1B), you have violated the independence axiom. To see, look at it closer:
We added the same new outcomes with their probabilities to both equally. Yet, our fundamental preferences changed.
Maurice Allais created the Allais Paradox in 1953 as a blistering critique of the independence axiom formulated by John von Neumann and Oskar Morgenstern in 1944. At its heart, it shows that humans change their preferences if the world changes slightly. That is a stab in the heart of the entire theory.
Section 5: Introspection
What then can we say is the use of the independence axiom? If reality were like the Allais Paradox — gambles with 100% certainty and a small addition of risk changing my fundamental preference — then all the classic results of expected utility theory, from pricing stocks and bonds to choosing an optimal foreign policy, are meaningless.
One counterargument is that the Allais Paradox does not conform to reality. Maybe many, if not most, gambles don't have outcomes with a 100% chance of happening. Or even if they do, the world changes the probabilities to be more than the small 1% or 2%.
Another argument going back to Savage, the founder of subjective utility theory, is that the independence axiom is a self-reflective guide. Someone trying to price a stock or bond or trying to win a game can't do better than thinking only and coherently about the probabilities and their outcomes. We can have our cognitive biases, fears of the unknown, and dislike of small additions of changes – but the prize is millions of dollars. We have to strip away the emotions and go back to the basics. The gambles did not fundamentally change when probabilities were added, so why change ourselves?3
The notion of introspection is the argument for why, in the long term, the stock market is rational. If someone tries to price a stock outside the norms of the expected utility function, then, eventually, reality will catch up to them. Those who are smart and stay within the bounds of expected utility will win over those who don't, whether in the stock market or even a game of Blackjack, Poker, or foreign policy.
Conclusion
Our world runs by risk. The events of the future, whether the flip of a coin or the rise or fall of a stock, can never be fully known. But we can know the probabilities and the outcomes and act accordingly. The three rationality axioms, suited for gambles, and the independence axiom allow for a new form of decision-making. It is one where our utility from a gamble comes from the probabilities and our own subjective valuation of them. From there, all else follows.
There are many ways that the independence axiom can fail. The Allais Paradox is the most classic result, but it is not the only one. Amos Tversky and Daniel Kahneman listed numerous psychological experiments showing ways the independence axiom fails in laboratory experiments. Yet even if it fails in many ways, it cannot be dismissed out of hand. Other work by researchers such as Mark Machina put the axioms on alternative theoretical footing. But the classic result of the independence axiom remains the standard and classic of the field. 4
The following articles on financial economics and game theory all rely one way or another on the axioms of this article. Yet their deficits should be kept in mind. With the crashes of the stock market, it is too simple to say that the four axioms are always true. It is too simple to say they are always false. They just are.
The information about independence axiom and expected utility comes from Microeconomic Theory by Andreu-Mas Colell, Michael Whinston, and Jerry Green. Oxford University Press, 1995.
I once went to the Pequot Museum in Mystic, CT. One of the exhibits showed Native men prior to the arrival of the Europeans playing a game of chance where they would bet with each other over who would win. Gambles are linked to human nature, it seems.
The argument is in The Foundation of Statistics by Leonard Savage, 1954, reprinted in 1972 by Dover Publications.
Choice under Uncertainty: Problems Solved and Unsolved by Mark Machina in Journal of Economic Perspectives Volume 1, 1987; “Expected Utility” Analysis Without the Independence Axiom by Mark Machina in Econometrica Volume 50, 1982; Prospect Theory : An Analysis of Decision Under Risk by Daniel Kahneman and Amos Tversky in Econometrica Volume 47, 1979